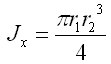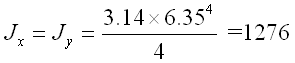Indirizzo articolo originale:
https://www.baronerosso.it/modellismo_articoli/show/685/calcolo-strutturale-del-tubo-coda.html
https://www.baronerosso.it/modellismo_articoli/show/685/calcolo-strutturale-del-tubo-coda.html
Calcolo strutturale del Tubo Coda
Adoperando qualche semplice formula matematica, vediamo come dimensionare correttamente il tubo di coda di un aeromodello
|
Un po' di scienza delle costruzioni Seguendo un post sulla forma dei tubi in carbonio che si usano per fare il trave di coda degli F3K ed anche d'altri modelli, mi è venuta l'idea di scrivere qualcosa che possa essere comprensibile senza andare oltre il concetto di radice quadrata, diciamo alla portata di tutti in questo Forum. Se prendiamo un tondino di alluminio pieno (o qualsiasi altro materiale omogeneo) e lo paragoniamo ad un tubo dello stesso diametro esterno, noteremo facilmente che quest'ultimo è più flessibile o se vogliamo debole qualsiasi sia lo spessore della sua parete. Ovvero, sarà in grado di sopportare sforzi più limitati soprattutto a flessione. Il tubo ovviamente sarà più leggero del tondino e, siccome per noi aeromodellisti è essenziale contenere i pesi, cerchiamo di capire se e soprattutto quanto convenga adottare una sezione piuttosto che un'altra a parità di materiale usato. Ecco che ci viene in aiuto la scienza delle costruzioni con il concetto di "Momento d'Inerzia". Esso è semplicemente un numero legato alla forma e dimensioni della nostra sezione. Una volta messo in relazione con le caratteristiche del materiale adottato, ci permette di risalire alle sollecitazioni che la nostra struttura potrà sopportare. Ora non voglio, in questa sede, dare indicazioni su come dimensionare la nostra struttura perché sarebbe il campo specifico della scienza delle costruzioni e presuntuoso da parte mia pretendere di farlo. Tuttavia vorrei introdurre qualche concetto che consenta di mettere il materiale dove lavora meglio senza peraltro rinunziare a dare qualche parametro dimensionale in termini di comparazione. Mettiamo a paragone in prima analisi un listello a sezione rettangolare (fig.1) 8x16 (centimetri o millimetri o quello che volete) con un tondino pieno (fig. 2) di diametro 12,7 di materiale omogeneo. Essendo le aree delle sezioni eguali potremo dire che hanno lo stesso peso o più precisamente la stessa massa, noteremo peraltro che, mentre il tondino flette allo stesso modo comunque lo giriamo, il listello fletterà meno se cerchiamo di piegarlo di taglio piuttosto che di piatto. Ovvio quindi che il suddetto "Momento d'Inerzia" sarà diverso a seconda della direzione secondo la quale sollecitiamo il nostro materiale. |
|
Risparmiandovi i passaggi matematici, peraltro semplici, vi do direttamente le formulette per calcolare il momento d'inerzia nei due casi. Esse sono, nel caso della sezione rettangolare, rispetto ai due assi baricentrali principali (invertendo semplicemente l'altezza con la base dato che la figura è asimmetrica): |
|
|
|
E, nel caso di quella circolare: |
|
|
|
E di quella ellittica dove r1 ed r2 sono i due raggi: |
|
|
|
Ovvero rispettivamente per la sezione rettangolare: |
|
|
|
e per la sezione circolare: |
|
|
|
Abbiamo così scoperto, anche se ce lo aspettavamo, che, a parità di peso, la sezione rettangolare in un senso reagisce meglio di quella circolare e nell'altro peggio ed anche di quanto (circa il doppio in un senso e la metà nell'altro). Infine, se analizzassimo bene le formulette, potremmo desumere che il materiale reagisce tanto meglio quanto più è lontano dall'asse in particolare con il cubo della distanza dal baricentro!!! |
|
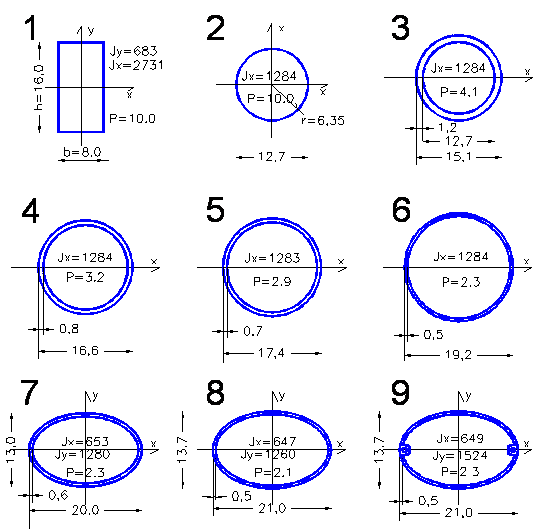
Se la sezione fosse cava, come un tubo quadro o tondo che sia, per avere il momento basterebbe sottrarre da quello della sezione piena, quello del cavo. Quando poi si tratta di figure complesse dove sarebbe lungo eseguire il calcolo viene in aiuto Santo "Autocad" che calcola automaticamente tutti i parametri di un solido o, come nel nostro caso, della sezione (vista come una Regione, vedi nota1) I valori del Momento d'Inerzia servono nella scienza delle costruzioni, conoscendo le caratteristiche del materiale, a determinare gli sforzi cui può resistere il nostro longherone o tubo che sia. Tuttavia, poiché questa operazione è più complessa, ci limiteremo, come si è detto, a paragonare due o più tubi o longheroni fra di loro mantenendo costante il Momento D'inerzia ed osservando come cambia la massa ovvero il peso. Mettiamo dunque a paragone diverse sagome create badando di mantenere pressappoco lo stesso Momento d'Inerzia intorno al valore 1284 a parte l'ultima pari a 1524 (capiremo poi perché). |
|
|
|
Facciamo quindi alcune considerazioni: Avendo tutte lo stesso Momento d'Inerzia vuol dire che reagiscono allo sforzo in modo analogo e possono equivalersi strutturalmente in un trave di coda o altrove. Tuttavia la massa P (ovvero un numero proporzionale alla superficie tanto ci interessa solo il paragone) varia molto, per la precisione da 10 del tondino pieno a 2, 1 della sagoma ellittica a dimostrazione di quanto sia importante la distribuzione del materiale. Le forme circolari, come si è detto, hanno un solo Momento rispetto all'asse x in quanto non varia comunque giriamo l'asse, quelle ellittiche ne hanno due, rispetto all'asse minore ed a quello maggiore. Significa ovviamente che queste ultime sono fatte per reagire meglio in un senso piuttosto che nell'altro, come si richiede nei modelli F3K che hanno bisogno di grande rigidità orizzontale al momento del lancio. Grosso modo il doppio nel senso orizzontale rispetto al verticale. Facciamo comunque attenzione a non esagerare perché dobbiamo pur sostenere l'elevatore! La sezione n°3 ha il diametro interno uguale al tondino pieno, spessore 1/10 del diametro e peso meno della metà! Un discorso molto attento richiede lo spessore della parete. Avrete notato che mentre un tondino pieno si spezza un tubo si schiaccia e si piega. Non si può assottigliare la parete oltre certi limiti. Anche se il Momento d'Inerzia mi dice che il tubo dovrebbe resistere allo sforzo cui intendiamo sottoporlo. Intervengono dei fattori di instabilità delle pareti sottili per cui la zona tesa resiste abbondantemente, mentre quella compressa no. Sarebbe difficile trovare lo spessore critico oltre il quale si rischia lo schiacciamento. Diciamo che 1/20 del diametro è un valore abbastanza prudenziale. Abbiamo parlato di materiale omogeneo, tuttavia è invalso l'uso di disporre le fibre longitudinalmente per resistere meglio alla flessione ma non dobbiamo dimenticare che, anche se in piccola quantità, dobbiamo disporre delle fibre in senso trasversale ed a 45° rispetto a quelle longitudinali perché esistono anche lo sforzo di taglio e soprattutto la torsione. Provate a prendere un mazzetto di spiedini o listellini, noterete che torcendolo fra le mani non opporrà alcuna resistenza. Se solo impedissimo lo scorrimento tra i vari elementi incollandoli tra di loro, la resistenza aumenterebbe ma c'è sempre il rischio che si stacchino (è quello che succederebbe usando solo fibre longitudinali) Cosa molto più saggia è invece quella di avvolgere il tubo con due spirali a 45° (inverse tra di loro in quanto la torsione può avvenire in entrambe i sensi) di fibra magari di kevlar o interporre un tessuto anche leggero sempre con la fibra a 45°. Noterete che la sagoma n°9, rispetto alla n°8 presenta due comodi canaletti laterali per il passaggio dei comandi realizzati in fase di costruzione, come ci suggerisce l'ing Gian Marco Occhiobove http://www.baronerosso.it/forum/categoria-f3k/74011-il-mio-nuovo-tipo-di-boom.html. E' significativo che, mentre il peso aumenta dell'11%, il Momento d'Inerzia aumenta del 21%, a dimostrazione, ancora una volta di quanto conti mettere il materiale più lontano possibile dal centro della sezione. |
|
Altra considerazione riguarda sempre l'idea dell'amico Gian Marco: Egli usa un'anima in polistirolo, sulla quale avvolgere le fibre di carbonio, che poi resta inglobata. Il contributo agli sforzi di flessione e torsione è veramente modesto, date le caratteristiche del materiale. Per altro verso, esso da un contributo notevole a vincere quella instabilità delle pareti sottili di cui sopra, consentendo uno spessore minore delle stesse. Chiedo scusa agli esperti della materia se, nel tentativo di semplificare e rendere digeribile un argomento importante e complesso, ho omesso una serie di cognizioni che stanno a monte dell'argomento e sono andato al sodo senza troppi preamboli. Ritengo che un impatto con un problema concreto sia il modo più semplice di affrontare, in prima battuta, argomenti complessi. Spero soprattutto di aver seminato curiosità in coloro che vorranno approfondire sugli opportuni testi e magari passare al dimensionamento vero e proprio. Buon lavoro a tutti, Favonio. Nota 1 Se avete un po' di dimestichezza con "Autocad" potete ricavare il momento d'inerzia di una figura a vostro piacere selezionando la figura stessa con il comando Proprietà massa/regione dal menù Strumenti sottomenù Interroga. Se cliccate con tale comando attivo su una Regione si apre una finestra con tutti i dati possibili ed immaginabili a cominciare dalla superficie (o volume nel caso di un solido) per finire ai moneti d'Inerzia rispetto agli assi baricentrali, che in questo momento ci interessano. Trasformate prima la vostra figura (attenzione che sia chiusa) con il comando Regione dal menù Disegna. Questo è quello che Autocad restituisce per l'ellisse n°9
Per i più curiosi allego il file dwg che mi è servito per calcolare i momenti. |
||||||||||||||||
|
|
Indirizzo articolo originale:
https://www.baronerosso.it/modellismo_articoli/show/685/calcolo-strutturale-del-tubo-coda.html
https://www.baronerosso.it/modellismo_articoli/show/685/calcolo-strutturale-del-tubo-coda.html