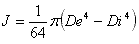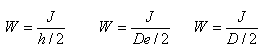Indirizzo articolo originale:
https://www.baronerosso.it/modellismo_articoli/show/577/le-baionette-alari.html
https://www.baronerosso.it/modellismo_articoli/show/577/le-baionette-alari.html
Le Baionette Alari
Un confronto sui vari tipi di baionette comunemente utilizzati e commercialmente reperibili indicandone sommariamente i pregi ed i difetti.
|
|
|
Le baionette in un modello ed in particolare in un aliante rappresentano da sempre una piccola incognita in fase progettuale. Le sollecitazioni sono difficilmente calcolabili senza perdersi in calcoli fuori dalla portata del modellista comune e di conseguenza ci si orienta sulla base di esperienza propria od altrui; tuttavia rimangono sempre dubbi e timori prima di effettuare una richiamata decisa o una manovra che solleciti particolarmente ali e baionetta e che spesso viene compiuta involontariamente per salvare il modello. Questo breve articolo non ha l'intenzione e la presunzione di dare delle indicazioni sulla scelta e sul dimensionamento della baionetta ma intende mettere a confronto i tipi di baionette comunemente utilizzati e commercialmente reperibili indicandone sommariamente i pregi ed i difetti. |
|
Usualmente le baionette alari che si possono comprare nei negozi di modellismo o che si trovano montate su modelli sono a sezione tonda o rettangolare. Spesso si pensa solo alla resistenza come caratteristica che una baionetta deve possedere e si potrebbe cercare di fare un raffronto per cercare un'equivalenza dimensionale a parità di resistenza tra le due tipologie; prima però cercheremo di analizzare altri aspetti che possono far scegliere tra i due tipi di baionetta. Un aspetto fondamentale da considerare è il luogo dove verrà abitualmente usato il modello: parlando di alianti le alternative sono pendio e pianura. Il volo in pianura è generalmente meno stressante per la struttura di un modello e gli atterraggi avvengono spesso posando dolcemente in planata il modello su un verde praticello piano ed uniforme; in pendio per contro spesso si atterra su dossi, arbusti e sassi e la classica musata nel terreno è sempre in agguato. Risulta quindi palese che per chi vola in pianura è importante dimensionare la baionetta solo in funzione del volo mentre in pendio si sente anche la necessità di non piegarla ad ogni atterraggio brusco. Il primo pensiero per risolvere questo problema potrebbe essere quello di dotare il modello di un bel baionettone tondo sovradimensionato che non si piegherà mai. No, niente di più sbagliato! Prima o poi la baionetta tonda si piegherà a meno di non usare un diametro veramente esagerato ma a questo punto sorgerebbero evidenti problemi di peso. Bisogna che la baionetta resista nel senso della flessione dell'ala ma sia cedevole e poco rigida nell'altra direzione permettendo quindi alle ali di spostarsi in avanti durante un urto violento attutendo tra l'altro il colpo; non dimentichiamo però di rinforzare opportunamente la fusoliera in zona karman (cosa che andrebbe sempre e comunque fatta) con due ordinate o due traversini posti al bordo di entrata e di uscita onde evitare che le ali schiaccino la fusoliera. La sezione rettangolare, utilizzata di costa (lato maggiore del rettangolo posizionato verticalmente), è quella che ci permette di avere le caratteristiche appena indicate in quanto la resistenza è maggiore nel senso del lato maggiore e notevolmente inferiore nell'altro; a seguito di un urto, anche se piegata, riuscirete sempre a raddrizzare ed estrarre una baionetta rettangolare mentre una tonda sarà difficilmente raddrizzabile e sarete costretti nei casi peggiori a rompere la fusoliera e cambiare il porta-baionetta. Come detto per chi vola in pianura questo non è fondamentale perché quando arriva il fatidico crash i danni sono molto ingenti e la baionetta è forse l'ultimo problema. Tuttavia la baionetta tonda presenta anche alcuni (pochi) vantaggi: durante la costruzione è più semplice posizionarla (fare un foro circolare con un po' di attenzione è in fondo più semplice e rapido) e comunque una volta assemblato il modello si ha sempre la possibilità di cambiare l'angolo di calettamento (incidenza) dell'ala solo spostando le spine di centraggio, ruotando quindi l'ala sulla baionetta; una rettangolare va invece riposizionata comunque anche per minime variazioni; in entrambi i casi è evidente che viene perso l'allineamento dell'ala col karman. Il peso è nettamente a favore della sezione rettangolare: a parità di resistenza a flessione una baionetta tonda pesa di più; tanto per fare un esempio una 12x2mm pesa meno della metà di una tonda di diametro 8mm ed hanno resistenze paragonabili. C'è da dire tuttavia che a scapito del portafoglio è possibile sostituire il tondino di acciaio armonico con un tondino di carbonio di pari diametro. In questo modo si riesce a risparmiare notevolmente peso e ad evitare il problema della baionetta irrimediabilmente piegata in quanto il carbonio essendo molto rigido si spezza a seguito di un urto violento; però visti i prezzi se prevedete di dare spesso musate ve lo sconsiglio. Le baionette di carbonio invece sono molto utili per i piani di quota dove ogni grammo di peso risparmiato si traduce in risparmio di piombo nel muso per il centraggio. Un vantaggio della baionetta tonda risiede nel fatto di richiedere dimensioni minori a parità di resistenza; di conseguenza su modelli di dimensioni ridotte dove lo spessore del profilo è esiguo sarà più difficile utilizzare una baionetta rettangolare tanto più se l'ala è costruita in struttura e si deve contemplare anche l'eventuale spessore dei longheroni alari. In modelli di dimensioni maggiori a volte si trovano anche baionette a tubo di dimensioni generose: in tal modo si risolve il problema del peso e si sfruttano i vantaggi della baionetta tonda; per contro una baionetta a sezione tubolare può essere soggetta anche a schiacciamento e punzonamento (schiacciamento locale ad opera di una carico concentrato molto intenso come quello che può derivare dallo spigolo di un porta baionetta). In definitiva la sezione rettangolare è quella che ottimizza al meglio il materiale, resistendo maggiormente nella direzione che ci interessa; per contro la tonda è più facilmente utilizzabile e reperibile e per questo spesso viene preferita soprattutto nei kit commerciali. |
|
Affrontiamo ora, con l'aiuto di alcune formule, il problema di come giungere al confronto fra le resistenze delle due tipologie di sezione. Iniziamo col definire le dimensioni delle varie baionette: |
|
|
|
Definiamo ora anche la sollecitazione che verrà presa in considerazione, cioè il momento flettente M: è quella coppia (forza moltiplicata per una lunghezza, immaginate una forza che cerca di far compiere una rotazione) generata dalle ali che fanno flettere appunto una sbarra, la baionetta, come in figura |
|
|
|
Consideriamo ora tutte le baionette che andremo ad esaminare sollecitate dal medesimo momento flettente M e costituite dallo stesso materiale caratterizzato da tensione di snervamento  (la tensione è una forza per unità di superficie; la tensione di snervamento è quella tensione per cui l'acciaio subisce deformazioni plastiche, ossia si piega definitivamente).Ogni sezione è caratterizzata da un'area A e da due assi detti principali d'inerzia che, se la sezione è doppiamente simmetrica, altro non sono che gli assi di simmetria; rispetto a questi assi si può calcolare il momento d'inerzia J: |
|
|
|
avendo indicato con d la distanza dell'infinitesimo elemento di area dA dall'asse principale d'inerzia considerato. |
|
Senza dare troppo peso a questa formula, consideriamo J come quell'entità che tiene conto di come è distribuito il materiale della sezione rispetto all'asse intorno al quale si ha flessione. In pratica è quel parametro che tiene conto della forma della sezione. Con riferimento ai simboli della figura precedente e considerando l'asse principale d'inerzia orizzontale, i momenti di inerzia per le tre sezioni in esame sono: |
||||||
|
||||||
|
Si può ora agevolmente determinare la tensione  che il momento flettente M produce nelle varie sezioni: |
||||||
|
|
||||||
|
avendo indicato con y la distanza dall'asse principale di inerzia. Risulta a questo punto evidente che la massima tensione si avrà nel punto più lontano dall'asse ovvero per y=h/2, y=De/2 e y=D/2 rispettivamente per i tre tipi di sezione. |
|
Quando la tensione della fibra più sollecitata (per quanto appena detto quella più lontana) eguaglierà la tensione di snervamento , caratteristica di ogni materiale, la baionetta si piegherà. In definitiva a noi interessa solo lo stato della fibra estrema per sapere quando inizierà a collassare il materiale; definiamo allora i moduli di resistenza elastici W per le tre sezioni considerate tramite le seguenti formule: |
|
|
|
E quindi la formula che esprime la tensione diventa: |
|
|
|
ed è riferita solo alla parte della sezione più lontana dall'asse; ovviamente è il punto dove la tensione è massima. Come già detto all'aumentare di M, aumenta proporzionalmente anche la tensione fino ad arrivare a nel punto di massima sollecitazione: in questo istante la sezione ha espresso il massimo momento resistente, cioè ha opposto la massima resistenza contro una forza che cerca di piegarla.Proviamo ora a vedere la formula precedente in un'altra maniera (portando W al primo membro ed invertendo i membri) ed inserendo al posto di  : |
|
|
|
In questo modo possiamo trovare quale sezione, nell'istante in cui la fibra più sollecitata arriva allo snervamento, esprima maggiore momento resistente; semplicemente quale resista di più ed è naturalmente quella con W più alto. |
| Di seguito vengono riportati i moduli di resistenza elastici W delle sezioni maggiormente utilizzate in campo aeromodellistico ed i pesi per unità di lunghezza. | ||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
Ora avete un termine di paragone tra i vari tipi di baionette, a voi la scelta! Un'ultima doverosa considerazione dopo tutti questi discorsi sulle baionette va fatta a riguardo delle guaine porta baionetta; queste devono essere di materiale adeguato (ottone), con tolleranze dimensionali adeguate in modo da non produrre fastidiosi giochi, ben dimensionate come lunghezza e annegate in cassonetti impegnanti tutto lo spessore del profilo, quindi in completo contatto con i rivestimenti, e sufficientemente lunghi per trasmettere dalle ali alla baionetta le sollecitazioni (circa 10% della semiapertura in ogni semiala per la baionetta e relativa guaina e 20% per il cassonetto che volendo, per i modelli più sollecitati, può essere ulteriormente prolungato e diventare un vero e proprio longherone a tutto spessore). Se non sarà assicurato un solido e robusto trasferimento degli sforzi potrete avere la baionetta più resistente ma vi si chiuderanno comunque le ali alla prima sollecitazione violenta o atterraggio brusco. Giorgio Un ringraziamento a Tullio A. (FAI4602), Tullio B. e Franco C. per i preziosi consigli (in ordine alfabetico per cognome). |
Indirizzo articolo originale:
https://www.baronerosso.it/modellismo_articoli/show/577/le-baionette-alari.html
https://www.baronerosso.it/modellismo_articoli/show/577/le-baionette-alari.html