Indirizzo articolo originale:
https://www.baronerosso.it/modellismo_articoli/show/514/bilanciare-un-aereo-senza-sospenderlo.html

Bilanciare un aereo senza sospenderlo
Un interessante articolo su come bilanciare il modello in maniera "inusuale"

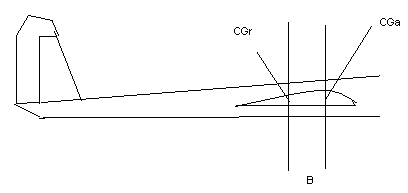
Voglio presentarvi un metodo semplice ma efficace che vi permetterà di bilanciare il proprio modello senza sospenderlo, ma solo effettuando misure "statiche".
Come tutti sappiamo infatti affinché un modello possa volare il centro di gravità statico deve coincidere con il punto di applicazione della portanza. In realtà di solito si fa in modo che il modello abbia una tendenza a picchiare, e cioè che il centro di gravità sia leggermente più in avanti del centro di spinta. Comunque per il calcolo che seguirà supporremo di voler far coincidere il centro di gravità statico con quello aerodinamico.
Il punto di applicazione della forza portante è di solito indicato dal progettista sugli schemi costruttivi, mentre il vero centro di gravità del modello dipende da come durante la costruzione abbiamo collocato i vari pesi a bordo, e cioè dove abbiamo messo le batterie, il motore, la radio, i servi, con quali materiali abbiamo realizzato le varie parti componenti la struttura portante e le ali.
Solitamente il centro di gravità è situato ad un terzo dell'ala dal bordo di attacco anteriore ma, ovviamente in base alla forma delle centine e ad altri parametri può essere leggermente spostato in avanti o indietro.

Per chiarire meglio questi concetti osserviamo il disegno seguente

Fig.1-BilanciamentoAereo

Supponiamo che il progettista ci indichi che la portanza sia applicata al punto CGa, mentre dopo aver costruito il modello il vero centro di gravità risulti nel punto CGr. Chiamiamo B la distanza tra il punto CGa e CGr.
Nel centro di gravità CGr verrà quindi applicata la risultante di tutti i pesi distribuiti sul modello. In pratica se il peso complessivo del modello fosse P, potremmo rappresentare P come un vettore applicato al punto CGr e diretto verso il basso. Durante il volo la portanza A verrà invece applicata al punto CGa e potremo rappresentarla come un vettore diretto verso l'alto. Rispetto al punto CGr nascerà quindi un momento di rotazione antioraria che tenderà a far sollevare il muso del modello e la cui intensità sarà pari a B*A. Il nostro obiettivo sarà quello di far in modo che B sia nullo e che quindi CGr e CGa coincidano.

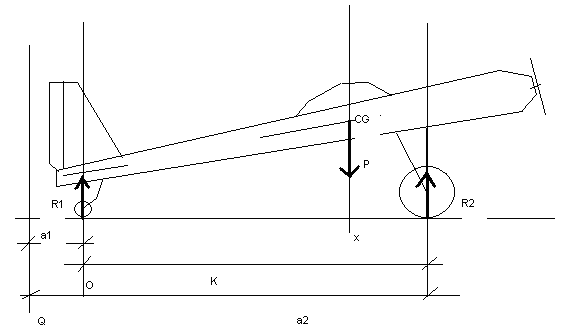
Per prima cosa dovremo acquisire il peso P complessivo del modello, successivamente dovremo collocare il modello su di un piano orizzontale e misurare la distanza tra il punto di appoggio del ruotino di coda e l'interasse delle ruote anteriori. Chiameremo questa distanza K. Per maggiore chiarezza osserviamo il disegno della pagina seguente:

Fig.1-BilanciamentoAereo

Ora è evidente a tutti che il modello collocato sul piano orizzontale è assolutamente immobile. In queste condizioni valgono le due equazioni fondamentali della statica :
  1. La somma di tutte le forze applicate deve essere nulla
  2. La somma di tutti i momenti rispetto ad un qualunque punto del piano deve essere nulla
In pratica considerato il peso del modello P, esso si scarica sui due punti di appoggio costituiti dalla ruota posteriore e dalle due ruote anteriori. Nei punti di appoggio nascono quindi delle reazioni vincolari dove risulta
R1 + R2 = P
R1 ed R2 possiamo misurarle mettendo sotto le ruote una bilancia. Il valore letto rappresenta la reazione del vincolo.

Prendiamo ora un qualunque punto Q in modo che sia esterno al segmento compreso tra le ruote anteriori e posteriori (per comodità di segno). Chiamiamo a1 la distanza dal punto Q ed il punto di appoggio della ruota posteriore, a2 la distanza del punto Q dall'interasse delle ruote anteriori ed x la distanza da Q del punto di incontro della perpendicolare al piano di appoggio passante per il baricentro del modello.

Per la seconda equazione della statica la somma dei momenti rispetto al punto Q deve essere nulla quindi possiamo scrivere:
a1 * R1 - x * P + a2 * R2 = 0
da questa equazione potremmo ricavare x in funzione dei valori R1 ed R2 letti. Per semplificare il calcolo osserviamo che la seconda legge della statica deve valere per qualunque punto del piano. Quindi vale anche per un punto O coincidente con il punto di appoggio del ruotino posteriore.
In questo caso rispetto al punto O l'equazione dei momenti si scrive come :
K * R2 - x * P = 0
dove questa volta x e K rappresentano distanze dal punto O.
Risolvendo questa semplice equazione rispetto ad x otteniamo
X = (K * R2) / P
L'equazione ottenuta possiamo utilizzarla in vari modi. Possiamo determinare deve cada il baricentro incognito di un modello misurando la reazione R2 ed il peso complessivo P, determinando x. Oppure conoscendo dove deve cadere il centro di gravita abbassare la perpendicolare al piano, misurare la distanza x1 dal ruotino posteriore e calcolare quale deve essere la reazione vincolare sulle ruote anteriori risolvendo rispetto ad R2.
R2 = (x1 * P) / K

Esempio
Per completezza facciamo un esempio numerico chiarificatore:

Il modello pesa 1.8 Kg
Abbassando la perpendicolare al punto dove deve cadere il baricentro misuriamo 70 cm di distanza dal ruotino posteriore. La distanza complessiva tra il ruotino posteriore e l’interasse delle ruote anteriori sia di 100 cm. Applicando l’equazione precedente determiniamo quale deve essere la reazione vincolare delle ruote anteriori:
R2 = (70 cm * 1.8 Kg) / (100 cm) -> R2 = 1.26 Kg
Potremo quindi collocare una bilancia sotto le ruote anteriori e regolare la disposizione dei pesi a bordo fino a quando la bilancia leggerà 1.26 Kg. A questo punto il modello sarà bilanciato. Se vorremo picchiarlo leggermente basterà leggere 1.27 Kg ed il gioco è fatto. In questo modo avremo spostato il baricentro in avanti e precisamente di 5.5 millimetri come possiamo calcolare :
X = (100 cm * 1.27 Kg) / 1.8 Kg -> X = 70.55
Ovviamente sarà meglio avere una bilancia elettronica.



Indirizzo articolo originale:
https://www.baronerosso.it/modellismo_articoli/show/514/bilanciare-un-aereo-senza-sospenderlo.html